S’entén per linealitat a tot allò que puga ser identificat o associat amb el comportament d’una línia recta. Així, si viatjo amb una velocitat de 50 km/h, puc assegurar que cada mitja hora hauré recorregut 25 km i que saber quina distància hauré recorregut d’ací a X hores és tan senzill com aplicar una regla de tres (tot i que només funcionarà si considerem la distància recorreguda des del punt de partida). La funció matemàtica que ho regeix és la funció lineal
La natura no és lineal
El cas és que a la natura hi ha infinitat de processos que no segueixen cap linealitat i intentar entendre’ls, representar-los o interpretar-los a partir d’ella ens porta al fracàs. Posem per exemple el creixement d’una xiqueta acabada de nàixer. Els primers mesos el creixement pot fer la sensació que és lineal, que creix tants centímetres cada X mesos, però és obvi que això deixarà de ser així prompte i acabarà per no créixer o, quan siga velleta, per decréixer. Ho vam veure també durant la pandèmia de Covid-19 amb el ritme de contagis, allò que semblava créixer de forma lineal al principi, de cop s’enlairava i fugia de la tendència que se li pressuposava des de la ignorància del comportament d’una altra funció matemàtica: l’exponencial.
Vegem-ho gràficament. A les figures es mostra la tendència de creixement en sumar de forma cíclica 2 unitats a una unitat inicial o de multiplicar per 2
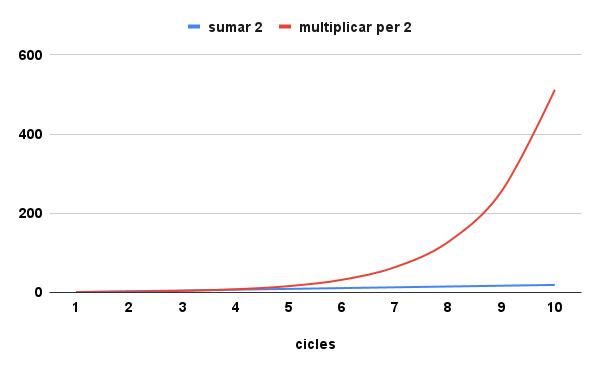
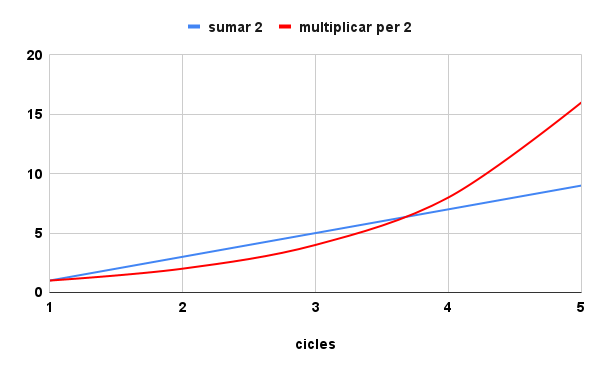
Com es pot veure a la figura 1, el comportament de la línia roja (multiplicar per 2, progressió geomètrica) s’allunya ràpidament del de la línia blava (sumar 2, progressió aritmètica) a partir del 5è o 6è cicle. De fet, fins aleshores la sensació és que es comporten igual. Si fem una aproximació (figura 2) a aquest tram (entre la situació inicial i el 5è cicle) veurem que la tendència d’ambdues progressions és similar fins al 4t cicle.
És per això que ens costa tant de diferenciar un comportament de l’altre en els seus inicis, i més si tenim con compte que potser els cicles tenen una durada temporal massa gran com per tenir en consideració allò que passarà a partir del 5è o 6è. Ara bé, altres vegades els cicles tenen una periodicitat més curta i aleshores ens trobem amb sorpreses.
La qüestió sobre la que voldria reflexionar, però, no és tant les diferències entre una funció matemàtica i l’altra sinó sobre el perquè de la nostra tendència a analitzar-ho tot des d’una perspectiva lineal. Resulta curiós perquè a la natura trobarem molts més exemples allunyats de la linealitat que no ajustats a aquesta.
La linealitat a l’aula
Com a professor de física i química m’he trobat amb un repte, per no dir-ne escull, cada vegada que un grup nou d’alumnes comença e estudiar la matèria a 2n d’ESO: la maleïda regla de tres. L’alumnat l’aplica amb fe cega davant qualsevol situació que se li planteja. Tot és susceptible de ser resolt mitjançant una regla de tres. L’han aprés a matemàtiques i li confereixen propietats gairebé miraculoses perquè ho resol tot, car quan l’estudien ho fan amb exemples on és d’aplicació, però que passa quan salten al món real? Doncs que es troben amb infinitat de realitats on la regla de tres no funciona. I el més greu, no entenen perquè ara els ha abandonat.
Ho deixo només com a hipòtesi perquè no he tingut ocasió d’experimentar-ho ni he sabut trobar bibliografia al respecte per si algú ho ha estudiat abans, però ¿què passaria si a primària i al primer cicle de secundària, en comptes d’explicar la regla de tres, s’explicara des d’un principi l’existència de diferents comportaments de les progressions amb tota mena d’exemples, i es donaren eines senzilles per a reconèixer-los?
Trobo que el fet d’interioritzar tan profundament la regla de tres de tan menuts ens porta a analitzar de forma inconscient tot el que ocorre al nostre voltant des d’aquesta perspectiva de la linealitat. Això ens impedeix d’identificar com cal certs processos a la natura que tenen conseqüències molt importants sobre les nostres vides: augment de la pol·lució i els residus, consum desmesurat, inviabilitat del nostre model de societat creixentista…
Algú s’anima a estudiar-ho?
